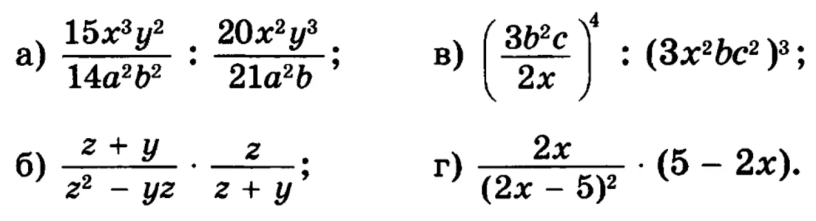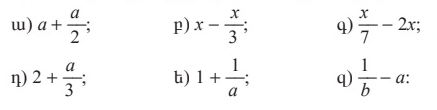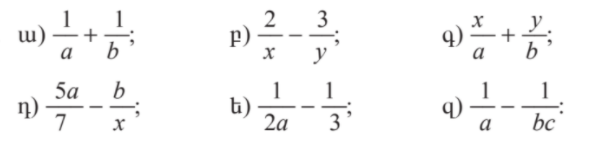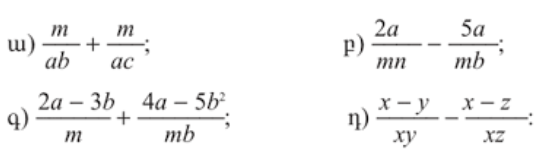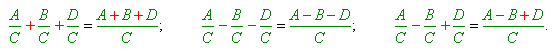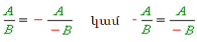Месяц: Декабрь 2023

Թեմա՝§14. Էներգիա: Մեխանիկական էներգիա

§15.Կինետիկ էներգիա

1.Ո՞ր մեծությունն է կոչվում էներգիա:

Էներգիայի մեծությունը կանոնավորված է լուսավորված էներգիայի հավասարումներով։

2.Բերել օրինակներ, որոնք ցույց են տալիս էներգիայի և աշխատանքի կապը:

Լուսամուտին թերակղումը: Երեխաներին աշխատանքային գործընկերները օգնում են մշակել բարձրացման սարքեր, իսկ լուսամ

3.Ի՞նչ միավորով է չափվում էներգիան ՄՀ-ում:

4.Մեխանիկական էներգիայի ինչ տեսակներ գիտեք:

Հիմա էներգիան չափվում է միջոցների միջոցով:

5.Ո՞ր էներգիան են անվանում կինետիկ:

Ներկայացված էներգիայի տեսակն այն է, որը գեներացվում է գեներատորի կողմից:

6.Ի՞նչ մեծություններից է կախված մարմնի կինետիկ էներգիան:

Մարմնի կինետիկ էներգիան կախված է միջոցառումներից, որոնք գեներացնում են այդ էներգիան: Այս միջոցառումները կարող են ներառել տեխնիկական աճի, ազդեցության մասնագետների գործումը, թվաքանակային կամայականությունը:

7. Ի՞նչ բանաձևով է որոշվում մարմնի կինետիկ էներգիան:

Մարմնի կինետիկ էներգիան որոշվում է հետազոտող տեղեկատվական նյութերի, ինչպես նաև սահմանվող մակարդակների և դրանց տարատերերի հետազոտողության միջոցով: Այդ տեղեկատվական միջոցները կարող են ներառել անձամբ միասին ենթարկվող մետաբույժները, հետևյալ՝ էներգիայի պարամետրերը, սալինացիայի ասպետները, հանքագուշակի ֆունկցիաները:

8. Ե՞րբ է մարմնի կինետիկ էներգիան զրո:

Մարմնի կինետիկ էներգիան զրո է եղելու վերջին գեղեցկության եպոսի վրայով, նաեւ մեկ մատուցման կամ խմբավորման ընթացքում: Սա կարող է տեղի ունենալ վարունակ պայմանագրով, որը կարող է տեղի ունենալ հետևյալ հատկությունների մեջ՝ անկախություն, զգուշացում, ապահովելու ուժի նորացում, առաջարկված հետևյալ բաժանորդագրերում: Հետադարձ կարող է անհապաղ վերածվել միջազգային նախաձեռնության մեջ։

9. Ինչպե՞ս է փոխվում մարմնի կինետիկ էներգիան

   ա. հավասարաչափ շարժման դեպքում,

   բ.  հավասարաչափ արագացող շարժման դեպքում,

   գ.  հավասարաչափ դանդաղող շարժման դեպքում:

10.Որ էներգիան են անվանում պոտենցիալ:

Պոտենցիալ էներգիան անվանվում է նաև թագքված անդամադրությունների երկարության ենթամատյան: Այն հեռավորված կենտրոններում է կիրառվում տեղակայված էներգիայի ստացման, պահածողի ուժի դեպքում։

11.Բերեք պոտենցիալ էներգիայով օժտված մարմինների օրինակներ:

12.Ինչ բանաձևով է որոշվում Երկրից որոշակի բարձրությամբ մարմնի պոտենցիալ էներգիան:

Պոտենցիալ էներգիայով օժտված մարմինների օրինակներ՝ հոգնական առողջության, աթլետիկ արտադրությունների և սպորտային արտադրությունների համար։

13.Փոխվում է արդյոք Երկրի մակերևույթին զուգահեռ թռչող մարմնի պոտենցիալ էներգիան:

Եկամուտը կարելի է ունենալ արդյոք զուգահեռ թռչող մարմնի պոտենցիալ էներգիան:

14.Մարմինն ընկնում է որոշակի բարձրությունից: Ինչպես է փոխվում նրա պոտենցիալ էներգիան անկման ընթացքում:

Նախկինում մարմինն է՝ պոտենցիալ էներգիան մեկ տեսակից մյուսի վրա հիմնավորելով: Ներկայացման ընթացքում մարմինը ընդգրկվում է զգացումների, վիրավորությունների, մուկների եւ այլն։ Կանոնակարգում է այնտեղ, որ մարմինը ամենօրյա հասակում առաջնորդվում է շարժումների եւ զգացումների։

15.Ինչպես կարելի է համոզվել, որ սեղմված զսպանակն օժտված է պոտենցիալ էներգիայով:

Այն կարելի է համոզվել սեղմված զսպանակի առանձնացման ժամանակացույցով կամ հեռախոսազանգով օգտագործելով այդ զպանակը։

16.Կատարելով անհրաժեշտ չափումներ՝ հաշվեք սեղանին դրված որևէ առարկայի պոտենցիալ էներգիան հատակի նկատմամբ:

Սեղմված զսպանակի ընդլայնումը կարելի է նկատել բարձր բլուր, բարձր գումարային էներգիայի աճ և թափանցիկ ընդլայնում։

ա)A=2
բ)A=40
գ)A=12
դ)A=-75
ե)A=5b
զ)A=36x²y

2․ Արտահայտությունը գրել կոտորակի տեսքով․

ա)3a/2
բ)2x/3
գ)-13x/7
դ)6+a/3
ե)a+1/a
զ)1-ab/b

3․Ձևափոխել հանրահաշվական կոտորակի․

ա)a+b/ab
բ)2y-3x/xy
գ)xb+ay/ab
դ)5ax-7b/7x
ե)3-2a/6a
զ)bc-a/abc

Advertisement

4․ Ձևափոխել հանրահաշվական կոտորակի․

ա)bm+cm/abc
բ)2ab-5an/mnb
գ)2ab-8b²+4a/mb
դ)xz-xy/xyz

5․Ձևափոխել հանրահաշվական կոտորակի․

ա)-x/8
բ)7a/24
գ)2m²-6m/6
դ)5a-2/30
ե)11x+9/24
զ)5a-13/30

6. Կատարել գործողությունները․

а)1/3
б)6y
в)4ab
г)???

7․Կատարել գործողությունները․

1)2/3x
2)6axy
3)13xm/3n
4)3x/y
5)11x²/3ab
6)4a³/5by

Թեմա՝ Հանրահաշվական կոտորակների բազմապատկումը և բաժանումը:

Կոտորակը կոտորակով բազմապատկելու համար պետք է համարիչը բազմապատկել համարիչով, իսկ հայտարարը՝ հայտարարով և առաջին արտադրյալը գրել համարիչում, իսկ երկրորդը՝ հայտարարում:

Հանրահաշվական կոտորակների արտադրյալը նույնաբար հավասար է մի կոտորակի, որի համարիչը հավասար է համարիչների արտադրյալին, իսկ հայտարարը՝ հայտարարների:

Եթե հնարավոր է, ապա ստացված կոտորակը կրճատում են:

Արտադրյալը սահմանվում է փոփոխականի միայն այն արժեքների համար, որոնց դեպքում կոտորակների հայտարարները հավասար չեն զրոյի:

Այսինքն՝ եթե A/B -ն և C/D -ն երկու հանրահաշվական կոտորակներ են, որտեղ A -ն, B -ն, C -ն և D -ն բազմանդամներ են, ապա A/B⋅C/D=A⋅C/B⋅D, որտեղ B≠0,D≠0:

Օրինակ

Կատարենք բազմապատկումը՝ 12a⁴/25b³⋅(−5b²/6a⁴)

Լուծում: Դրական և բացասական թվերի արտադրյալը բացասական թիվ է, այդ պատճառով կոտորակի առջևում դնում ենք մինուս նշանը:

Որպեսզի մի կոտորակ բաժանել մյուսի վրա, պետք է համարիչի կոտորակը բազմապատկել հայտարարի կոտորակի հակադարձ կոտորակով:

Օրինակ

Նույն կանոնը գործում է նաև հանրահաշվական կոտորակների դեպքում՝ կոտորակները բաժանելու համար պետք է համարիչի կոտորակը բազմապատկել հայտարարի կոտորակի հակադարձ կոտորակով:

Եթե հնարավոր է, ապա համարիչի և հայտարարի արտահայտությունները վերլուծվում են արտադրիչների և կրճատվում:

Կանոնը մնում է ուժի մեջ, երբ արտահայտություններից մեկը բազմանդամ է: Այդ դեպքում պետք է բազմանդամը ներկայացնել 1 հայտարարով կոտորակի տեսքով:

Օրինակ

Հարցեր և առաջադրանքներ։

1․Ինչպե՞ս են բազմապատկվում հանրահաշվական կոտորակները։

2․Ինչպե՞ս են բաժանվում հանրահաշվական կոտորակները։

3․Կատարել գործողությունները․

4․Ձևափոխել հանրահաշվական կոտորակի․

5․Կատարել բազմապատկում և բաժանում․

6․Կատարել բազմապատկում և բաժանում․

Сочинение

Самый любимый и долгожданный праздник. В преддверие Нового года мною овладевает странное чувство, что должно случиться что-то волшебное и радостное. Повсюду атмосфера праздника, и люди готовятся к его приходу — покупают пышные ели домой, различные фрукты и сладости на стол, и конечно, подарки для своих близких. Для детей, Новый год — это настоящая сказка. Накануне Нового года мы начинаем готовиться к его празднованию. Украшаем нашу елку и комнаты яркими гирляндами и игрушками, мишурой и разноцветными шарами. Квартира преображается, становится праздничной и еще более уютной.

1.Տրված արտահայտություններից  յուրաքանչյուրով երկու նախադասություն կազմի՛ր` դրանք գործածելով

ա) ուղիղ իմաստով,
 բ) որպես դարձվածք:

Լեզուն չորանալ, ջուրը չտեսած`բոբիկանալ, ականջին հասնել:

Բավականաչափ ջուր չօգտագործելու դեպքում հաճախակի լեզուն չորանում է։

Փոքրիկները ծով գնալիս, ջուրը չտեսած բոբիկանում են ուրախությունից։

Ատամի ցավը սաստկանալու դեպքում կարող է ականջին էլ հասնել։

Լեզուն չորանար, որ այդպիսի արտահայտություններ չաներ նրա հասցեին։

Խորհուրդ կտաի շատերին ջուրը չտեսած չբոբիկանլ, ամեն ինչ կշռադատել և վերջում որոշում կայացնել։

նրա ականջին հասել էր այն, ինչը որ պետք է անակնկալ լիներ։
2.Ընդգծված դարձվածքները փոխարինի՛ր տեքստի ոճին հարմար հոմանիշ բառերով:

Մեր նախնիները երևի շատ դառը փորձերից հասկացել էին, որ ձուկ ուտելիս չի կարելի երկաթե դանակ գործածել: Այդ կանոնը ուշադրություն չդարցնող մարդիկ անկողին էին ընկնում ու նույնիսկ հոգին փչում: Հիմա արդեն գիտենք, թե ինչից էր  դա. երկաթը հեշտ քայքայվող սպիտակուցների հետ (ձկան մսի մեջ շատ կա) ռեակցիայի մեջ է մտնում, որի հետևանքով առաջանում է թունավոր նյութ:

Այսօր արդեն կենցաղում երկաթե դանակ չի օգտագործվում. Դարեր առաջ ստեղծվել է չժանգոտվող պողպատը, որը կարելի է առանց վախի օգտազործել: Բայց գյուտն ուշացել էր. այդ սովորության հետևանքով շատերն էին տուժել։ Հիմա ընդհանուր կարծիքն այն է, որ ձուկը դանակով ուտել չի կարելի:

3.Տրված բառերը բաժանի՛ր ըստ խոսքի մասի պատկանելության գոյական, ածական, թվական, դերանուն, բայ, մակբայ, կապ, շաղկապ, ձայնարկություն, վերաբերական բառեր (յուրաքանչյուրից երեք բառ):

Հարյուր իննսուներեք-թվական, թե-շաղկապ, դու-դերանուն, անշուշտ-Վերաբերական, դանդաղ-, վրա-մակբայ, թութակ-գոյական, բոլորը-գոյական, վա՜յ-ձայնարկություն, մասին, կամաց-կամաց-ածական, հավանաբար, մտերմանալ-բայ, հովիվ-գոյական, որպեսզի-շաղկապ, արագ, երրորդ-թվական, կացին-գոյական, ա՜խ-ձայնարկություն, դեղին-ածական, ընկերանալ-բայ, երկար-բայ, կարծես-վերաբերական, կրկնել-մակբայ, է՜-ձայնարկություն, բացի-մակբայ, որովհետև-շաղկապ, հինգական-թվական:

4.Հարցական դերանունները փոխարինի՛ր այնպիսի բառերով, որոնք ընդգծված առարկաներին (ենթականերին) ինչ-որ հատկանիշ վերագրեն:

Պարզվեց, որ գաղտագողի մոտեցող մարդը (ինչպիսի՞ն) ճաղատ է:
Քաղաքում պտտվող լուրերը (ինչպիսի՞ն) անսպասելի էին:
Եվրասիա մայրցամաքը (ո՞րն) ամենամեծն է:      
Խորհրդավոր այցելուները (քանի՞սն) յոթն են:
Այդ մրցույթի մասնակիցները (քանի՞սն) տասնվեցն են:
Մեր դպրոցը շրջանում (ո՞րերորդն) առաջատարն է:
Մեր արձակուրդը (ի՞նչ է անում)շատ լավ է անցնում:
Աշունը (ի՞նչ է արել) գունավորել է դաշտերը, այգիներն ու անտառները:

5.Բառակապակցություններ կազմի՛ր` Ա խմբի մակբայներն ավելացնելով Բ խմբի ածականներին ու բայերին:

Ա. Շատ, փոքր-ինչ, համարյա, հազիվ, ներքուստ:
Բ. Դեղին, հանգիստ, մեծ, հուզվել, հանգստանալ, լաց լինել:
Փոքր-ինչ հանգստանալ,
Շատ մեծ,
Համարյա դեղնել
Հազիվ լաց լինել
Ներքուստ հուզվել

ԹԵՄԱ՝  §13.Ռեակտիվ շարժում: Հրթիռային տեխնիկայի զարգացումը:

1. Ո՞ր շարժումն է կոչվում ռեակտիվ;                            

Ռեակտիվ շարժումը կամայական է արդյունքներում հանգույցների հետ բաժանվելու։  

2. Բերել ռեակտիվ շարժման օրինակներ:

Օրինակները՝ լեզվաբառերի և տեղանքների տեղադրումը երեք կամ ավելի հանգույցների համար համարվում է ռեակտիվ շարժում։

3. Ի՞նչ կառուցվածք ունի հրթիռը:

Հրթիռը ունի ստանդարտ շարժման չափերի և ազդեցության համակարգ։

4․ Բացատրեք, թե ինչպես է շարժվում հրթիռը։

Հրթիռը շարժվում է ներառյալ զարգացման միջոցների երկրաչափերով։

5. Կարո՞ղ է արդյոք հրթիռը շարժվել անօդ տարածությունում։ Իսկ կարո՞ղ է հրթիռն արգելակել  տիեզերքում (անօդ տարաությունում): Ինչպե՞ս:

Եթե ​​հրթիռը շարժվելու է անօդ տարածության մեջ, ապա այն կարող է վերածվել չափազանց առաջացնելու պահին, այնպես էլ տիեզերքում: Հրթիռը արգելվում է անօդ տարածության մեջ, եթե ​​այն գազային հիդրոդամ է պահում:

6․ Ի՞նչ գիտեք տիեզերագնացության հաջողությունների մասին։

Թեմպերատուրային դասընթացների, նախագծերի և ուսուցիչների շարժական հաջողությունները գիտելիս։

7. Կարո՞ղ է արդյոք իդեալական հարթ հորիզոնական սառույցի վրա կանգնած մարդը տեղից շարժվել՝ որևէ  ձևով չհրվելով սառույցից։

Արդյունքում, այդպես էլ, հարթ հորիզոնական սառույցի վրա կանգնած մարդը կարող է տեղից շարժվել արտաքին զարգացման համար, նույնպես էլ ներառյալ սառույցից։

79

80=

81-AF=3,5
AE=5
AO=3

82

14,6

83 Ըստ առաջին հայատանիշի միջնագծերը հավասար են։

85=

86=

Թեմա՝ Հանրահաշվական կոտորակների գումարումն ու հանումը

Հավասար հայտարարներով կոտորակների գումարման և հանման ժամանակ՝ գումարվում կամ հանվում են նրանց համարիչները, իսկ հայտարարները մնում են անփոփոխ:

Նույն կանոնով գումարվում և հանվում են հավասար հայտարարներով հանրահաշվական կոտորակները՝

• հանրահաշվական կոտորակների գումարման ժամանակ, համարիչները գումարվում են, իսկ հայտարարները մնում են անփոփոխ՝

• հանրահաշվական կոտորակների հանման ժամանակ, համարիչները հանվում են, իսկ հայտարարները մնում են անփոփոխ՝

Նույն կանոնով կարելի է գումարել կամ հանել հավասար հայտարարներով մի քանի կոտորակներ՝ 

Եթե կոտորակների հայտարարները հակադիր արտահայտություններ են, ապա դրանց գումարելու կամ հանելու համար պետք է սկզբում կիրառել հանրահաշվական կոտորակների նշանների փոփոխման կանոնը,

ապա գումարել կամ հանել հավասար հայտարարներով կոտորակները:

Դիտարկենք այն դեպքը, երբ հանրահաշվական կոտորակների հայտարարները իրարից տարբեր միանդամներ են, օրինակ այսպիսի՝ 

Այդպիսի հանրահաշվական կոտորակները գումարելու կամ հանելու համար պետք է՝

•  գտնել ընդհանուր հայտարարը,
•  որոշել յուրաքանչյուր կոտորակի լրացուցիչ արտադրիչը (ընդհանուր հայտարարի բերելիս),
•  գումարել կամ հանել նոր կոտորակների համարիչները,
•  հնարավորինս կրճատել ստացված կոտորակը:

Հարցեր և առաջադրանքներ։

1․ Ինչպե՞ս են գումարվում միևնույն հայտարարով հանրահաշվական կոտորակները։

Հավասար հայտարարներով կոտորակների գումարման և հանման ժամանակ՝ գումարվում կամ հանվում են նրանց համարիչները, իսկ հայտարարները մնում են անփոփոխ:

2․ Ինչպե՞ս են գումարվում հակադիր հայտարարներով հանրահաշվական կոտորակները։

Եթե կոտորակների հայտարարները հակադիր արտահայտություններ են, ապա դրանց գումարելու կամ հանելու համար պետք է սկզբում կիրառել հանրահաշվական կոտորակների նշանների փոփոխման կանոնը,

3․ Ինչպե՞ս են գումարվում տարբեր հայտարարներով հանրահաշվական կոտորակները։

Այդպիսի հանրահաշվական կոտորակները գումարելու կամ հանելու համար պետք է՝

•  գտնել ընդհանուր հայտարարը,
•  որոշել յուրաքանչյուր կոտորակի լրացուցիչ արտադրիչը (ընդհանուր հայտարարի բերելիս),
•  գումարել կամ հանել նոր կոտորակների համարիչները,
•  հնարավորինս կրճատել ստացված կոտորակը:

4․ Կատարել գործողությունները․

ա) x+y/3

բ) a-b/7

գ) 2x-3y/ 5

5․ Կատարել գործողությունները․

ա) x/2
բ) 3a-1/3
գ) 2a+b/5
դ) 2y-x/7

6․Կատարել գործողությունները․

7․ Պարզեցրել արտահայտությունը․

ա) 3/a
բ) a+3/x
գ) -a/b
դ) 5m+3n/4
ե) 4x/4=x
զ) 5a/8

8․ Կատարել գործողությունները․

ա) 8/a+b

բ) 1/x-1

գ)a6/a+b

դ) m2-2/m+n

ե) -x-9/x-3

զ) 8p-8/p+1