Թեմա՝ Հանրահաշվական կոտորակներ

Հարցեր և առաջադրանքներ
1.Գրեք հանրահաշվական կոտորակներիի օրինակներ։

4/5, 6/7, a/2b
2.Գրեք  անկրճատելի, անկանոն, կանոնավոր կոտորակների օրինակներ։
2/3, 3/2,
3.Գրեք այնպիսի հանրահաշվական կոտորակ, որն հնարավոր լինի կրճատել։
3/9
4.Գրեք այնպիսի հանրահաշվական կոտորակ, որը հնարավոր չլինի կրճատել։
6/7
5.Կազմեք այնպիսի հանրահաշվական կոտորակ, որն կրճատվի
ա) 2-ով

4/6
բ) a-ով

4a/ab
գ) ab-ով

8abc/dab
դ) 2a^3b-ով

6.Կոտորկաները դարձրեք 36x^2 հայտարարով․

5/36*1/x²
2/x²*1/36
11/3x*1/12x
7/9x²*1/4
1/4x*1/9x

7.Կոտորկաները դարձրեք 20x^2y հայտարարով․

1/20y*1/x²
5/x²*1/20y
7/20*1/x²y
11/2x*1/10xy
3/5xy*1/4x

8.Կոտորկաները դարձրեք նույն հայտարարով․

ա) 3x/6+2/6
բ) 7x/35+(-15/35)
գ) 12x/30+(-25/30)

9.Կոտորկաները դարձրեք նույն հայտարարով

ա) -x/(x-2)²+1/(x-2)²
բ) x/(5+x)²+-3/(5 +x)²

10. Կրճատեք կոտորակը

ա) a+b/c+d
բ) a+b/m+n
գ) x/(x+y)

Թեմա՝ Հանրահաշվական կոտորակներ

Հանրահաշվական կոտորակ կոչվում է A/B տեսքի արտահայտությունը, որտեղ A-ն որևէ բազմանդամ է, իսկ B-ն՝ ոչ զրոյական բազմանդամ:
Հիշեցում․ Բազմանդամ կոչվում է  միանդամների գումարը։

Բերենք մի քանի հանրահաշվական կոտորակների օրինակներ․
x/4
(a+b)/a
-5/(a+b+c+d) 
(a+b)/(a-b)

Հանրահաշվական կոտորակները օժտված են մի քանի հատկություններով․

Այսինքն.
I հատկություն
հանրահաշվական կոտորակի հայտարարի մեկը կարել է անտեսել։
Տես օրինակը․ (a+b)/1=a+b

II հատկություն․
հանրահաշվական կոտորակը չի փոխվում, երբ համարիչը և հայտարարը բազմապատկում ենք ոչ զրոյական նույն բազմանդամով։
Տես օրինակը․
(a+b)/(a-b)=(a+b)(d+2)/(a-b)(d+2)

III հատկություն․
հանրահաշվական կոտորակի առջևում դրված մինուս նշանը կարելի է տեղաշարժել համարիչ կամ հայտարար։
Տես օրինակը․
-(a+b)/(c+d)=(a+b)/-(c+d)

Հարցեր և առաջադրանքներ

1.Ի՞նչ է բազմանդամը, բերեք օրինակներ։

Բազմանդամ կոչվում է  միանդամների գումարը։

2.Ի՞նչ է հանրահաշվական կոտորակը, բերեք օրինակներ։

Հանրահաշվական կոտորակ կոչվում է A/B տեսքի արտահայտությունը, որտեղ A-ն որևէ բազմանդամ է, իսկ B-ն՝ ոչ զրոյական բազմանդամ:

3.Հանրահաշվական կոտորակները ի՞նչ հատկությամբ են օժտված, օրինակներով ցույց տվեք։

1 հատկություն
հանրահաշվական կոտորակի հայտարարի մեկը կարել է անտեսել։

2 հատկություն․
հանրահաշվական կոտորակը չի փոխվում, երբ համարիչը և հայտարարը բազմապատկում ենք ոչ զրոյական նույն բազմանդամով։

3 հատկություն․
հանրահաշվական կոտորակի առջևում դրված մինուս նշանը կարելի է տեղաշարժել համարիչ կամ հայտարար։

4.Կրճատեք կոտորակները․

ա) 1/2
բ) 2/3
գ) 3/14
դ) 64/231

5.Օգտագործելով հանրահաշվական կոտորակի հատկությունը, գրեք կոտորակը բազմանդամի տեսքով․

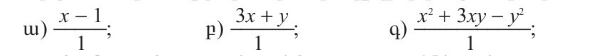
ա) x – 1
բ) 3x + y
գ) x^2 + 3xy – y^2

6.Կոտորակները բերեք ընդհանուր հայտարարի․

ա) 10/15, 12/15
բ) 21/28, 36/28
գ) 8/9, – 5/9
դ) 28/35, – 15/35
ե) 4/6, 5/6
զ) 13/14, 12/7
է) 7/9, – 15/9
ը) 2/5, – 5/10
թ) 9/30, 8/30

7.Կրճատեք կոտորակները․

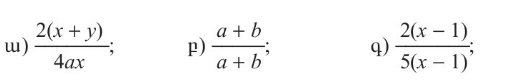
ա) (x + y) / 2ax
բ) 1
գ) 2/5

8.Կրճատեք կոտորակները․

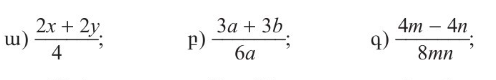
ա) (x + y) / 2
բ) (a + b) / 2a
գ) (m – n)/2mn

Առաջադրանքներ ամրապնդելու համար
1. Հաշվեք

ա) 1/16
բ) 1/3
գ) 1/81
դ) 1
ե) 9/20
զ) 1/9

2. Ստուգեք հավասարությունը

ա) Ճիշտ է
բ) Ճիշտ է

3. Հաշվեք

ա) 1/8
բ) -8
գ) -1/8
դ) -8
ե) 1/16
զ) 16
է) 1/16
ը) -16

4. Ներկայացրեք ամբողջ ցուցիչով աստիճաի տեսքով

ա) (a * b)^-3
բ) (7 * 0.5)^3

5. Ներկայացրեք ամբողջ ցուցիչով աստիճաի տեսքով

ա) a^6b^-15

բ) a^14b^-4

գ) a^12b^20

6. Համեմատեք

ա) >
բ) =
գ) >

7.Ներկայացրեք քառակուսու տեսքով

ա)(a^2)^2

ա)(a^10)^2

գ)(a^25)^2

8. Կատարեք բազմապատկումը

1)a^8
2)b^9
3)-m^6
4)-x^8
5)-y^11
6)c^11
7)p^n+2
8)a^m+4
9)x^n+k+3
10)y^n+5
11)z^3n – 2
12)b^-m+3

9. Բարձրացրեք աստիճան

1)a^6
2)x^8
3)-y^12
4)-x^20
5)-c^40
6)x^21
7)-y^45
8)b^12
9)z^3n
10)y^5k

Թեմա՝ Ամբողջ ցուցիչով աստիճանի հատկություները

Դիցուք a-ն և b-ն զրոյից տարբեր ցանկացած իրական թվեր են, իսկ m-ը և n-ը՝ ցանկացած ամբողջ թվեր։ Այդ դեպքում ճիշտ են հետևյալ հավասարությունները՝


Տես օրինակները


Առաջադրանքներ։
1. Գրեք ամբողջ ցուցիոչվ աստիճանի տեսքով.

ա) 2^3×2^4=2^3+4=2^7

բ) 5×5^6=5^1+6=5^7

գ) 4^3×4^2×4=4^3+2+1=4^6

դ) 7^2x7x7^5=7^2+^1+5=7^8

ե) 3^6×3^7x3x3=3^6+^7+1+1=3^15

զ) 6^4×6^4×6^3×6^2=6^4+4+3+2=6^13

է) 11^2×11^2×11^2=11^2+2=2

ը) 9^3×9^6×9^2×9^4×9=9^3+6+2+4=6^15

2. Գրեք ամբողջ ցուցիոչվ աստիճանի տեսքով.

ա) a^5^.a^4=a^5+4=a^9

բ) a^3^.a^8=a^3+8=a^11

գ) a^10^.a=a^10+1=a^11

դ) a^.a^7=a^8

ե) a^.a=a^1+1=a^2

զ) a^.a^2^.a^3^.a^4=a^1+2+3+4=a^10

3. Գրեք ամբողջ ցուցիոչվ աստիճանի տեսքով.

ա) 2^5:2^4=2^5-4=2

բ) 3^7:3^8=3^-1

գ) 5^9:5=5^9-1=5^8

դ) 10^3/10=10^3-1=10^2

ե) 5^7/5^13=5^7-13=5^-6

զ) 8^12/8^10=8^12-10=8^2
4. Գրեք ամբողջ ցուցիոչվ աստիճանի տեսքով.

ա) a^7:a^3=a^7-3=a^4

բ) a^8:a^12=a^8-12=a^-4

գ) a^6:a=a^6-1=a^5

դ) a^12/a^4=a^12-4=a^8

ե) a^20/a^22-a^20-22=a^-2

զ) a^20/a=a^20-1=a^19
5. Գրեք ամբողջ ցուցիոչվ աստիճանի տեսքով.

ա) 10^2/12^2=(10/12)^2

բ) 4^3/5^6=(2^2)^3/5^6=(4^6/5^6)

գ) 25^4/7^8=(5^2)^7/7^8=5^8/7^8=(5/7)^8

դ) (m^3)^4/(a^3)^3=m^12/a^12=(m/a)^12

ե) m^3m^5/a^8=m^3+5/a^8=m^8/a^8

զ) (n^6)^2/a^12=n^12/a^12

6. Գրեք ամբողջ ցուցիոչվ աստիճանի տեսքով.

ա) a^3^.a^4=a^3+4=a^7

բ) a^4^.a=a^4+1=a^5

գ) a^13:a^6=a^13-6=a^7

դ) a^12:a=a^12-1=a^11

ե) (a^4)^6=a^24

զ) (a^2)^5=a^1-

է) a^7^.b^7=(ab)^7

ը) a^4^.b^4=(ab)^4

7. Գրեք ամբողջ ցուցիոչվ աստիճանի տեսքով.

ա) a^5:a^6=a^5-6=a^-1

բ) a^7:a^6=a^7-6=a^1

գ) a^4:a=a^4-1=a^3

դ) a^12:a^12=a^12-12=a^0=1

ե) a^-4:a^6=a^-4-6=a^-10

զ) a^4:a^-5=a^4-(-5)=a^9

է) a^-11:a^-8=a^-11-(-8)=a^-3

ը) a^-4:a=a^4-1=a^-3

թ) a^6:a^5=a^6-5=a

ժ) a^9:a^0=a^9-0=a^9

ի) a^-3:a^0=a^-3-0=a^-3

լ) a^0:a^-8=a^0-(-8)=a^8

8. Աստղանիշի փոխարեն գրեք այնպիսի թիվ, որ հավասարությունը ճիշտ լինի.

ա 3^5x*=3^8

3^8:3^5=3^3

բ) 4^3x*=4^6

4^6:4^3=4^3

Թեմա՝ Ամբողջ ցուցիչով աստիճանի գաղափարը

Թվի (միանդամի) ցուցիչը, երբ բնական թիվ էր, մենք ուսումնասիրել ենք նախորդ ուսումնական տարում, այս տարի էլ հասցրել ենք մի քիչ  կրկնել, տես օրինակը

Երբևէ  մտածել ես ինչի՞ է հավասար այս արտահայտությունը, երբ թվի ցուցիչը բացասական թիվ է կամ զրո է

Պայմանավորվենք, այսուհետ բացասական ցուցիչով աստիճանը համարել՝


Օրինակներ Տիգրան





Կարևոր


Առաջադրանքներ

1. Հաշվեք․

ա) 1
բ)1
գ)1
դ )1

2. Հաշվեք․


ա) 2
բ) 1
գ)2^-1
դ)2^-2
3. Գրեք ամբողջ ցուցիչով աստիճանի տեսքով․

ա) 2³
բ) 2⁸
գ)3^-2
դ)4¹
ե)3^-1
զ)3^-4
է)5¹
ը)16^-1
թ)25^-1
ժ)2⁰
4. Հաշվեք․

ա) 10000, 1000, 100, 10, 1, 1/10, 1/100, 1/1000, 1/10000
բ) 32, 16, 8, 4, 2, 1, 1/2, 1/4, 1/8, 1/16
գ) -27, 9, -3, 1, -(1/3), 1/9, -(1/27)
5. Համեմատեք․

ա) =
բ) <
գ) <
դ) <
ե) >
զ) <

Թեմա՝ Քառակուսի

Սահմանում։ Քառակուսի կոչվում է այն ուղղանկյունը, որի բոլոր կողմերը հավասար են:

Քանի որ ուղղանկյունը զուգահեռագիծ է, ապա քառակուսին ևս զուգահեռագիծ է, ընդ որում այնպիսի զուգահեռագիծ, որի բոլոր կողմերը հավասար են, այսինքն՝ նաև շեղանկյուն է: Դրանցից հետևում է, որ քառակուսին օժտված է ինչպես ուղղանկյան, այնպես էլ շեղանկյան բոլոր հատկություններով:

Ձևակերպենք քառակուսու հիմնական հատկությունները.
ա) Քառակուսու բոլոր անկյունները ուղիղ են
բ) Քառակուսու անկյունագծերը հավասար են, փոխուղղահայաց են, հատման կետով կիսվում են և կիսում են քառակուսու անկյունները:


Հարցեր և առաջադրանքներ։
Ո՞ր պատկերն է կոչվում քառակուսի, GEOGEBRA ծրագրով գծեք ABCD քառակուսի։

Քառակուսի կոչվում է այն ուղղանկյունը, որի բոլոր կողմերը հավասար են:

2.GEOGEBRA ծրագրով գծեք ABCD քառակուսի, նշեք քառակուսու  կողմերը, անկյունագծերը։

3. GEOGEBRA ծրագրով գծեք ABCD քառակուսի, ինչպիսի՞ անկյուն են կազմում քառակուսու  անկյունագծերը։

4. Գտեք քառակուսու բոլոր անկյունների աստիճանային գումարը։ Ո՞ր բանաձևով ես հաշվում։

(4-2)x180=360
(n-2)x180

5. Նշեք քառակուսու մի կողմին առընթեր անկյունների գումարի աստիճանային չափը։

180

6. Նշեք քառակուսուն  բնորոշ որևէ  առանձնահատկություն։

7. Քառակուսու  մի կողմը հավասար է 21դմ է։ Գտեք քառակուսու պարագիծը։

21×4=84

8. Քառակուսու պարագիծը 72 սմ է: Գտեք քառակուսու կողմը:

72։4=18


10. Քառակուսու անկյունագծերի հատման կետից մինչև բոլոր կողմերը եղած հեռավորությունների գումարը 20 սմ է: Գտեք քառակուսու պարագիծը:

20:4=5
5×2=10
10×4=40


11․ Քառակուսու պարագիծը 80 սմ է: Որքա՞ն է քառակուսու անկյունագծի միջնակետի հեռավորությունը նրա կողմից։

80:4=20
20:2=10


12․ Շեղանկյան անկյունագծերից մեկը հավասար է կողմին: Գտեք շեղանկյան անկյունները։

180-60=120
60, 120, 60, 120

13․ Գտեք ABCD շեղանկյան պարագիծը, եթե ∠B = 60 աստիճան է, իսկ AC = 10,5 սմ:

10,5×4=42

Текст Левона Гамбуряна
Урок составила Моника Товмасян Трудно
сказать, что всего дороже на свете. У каждого человека свое понимание, свой подход к этому вопросу. Для кого-то дороже всего Родина, для другого – семья. Кто-то не может жить без друзей, а кто-то без своей собаки. Есть люди, для которых деньги – это все, а есть такие, кому личная свобода дороже всего на свете. Самое дорогое, что есть у меня — это моя семья, здоровая, крепкая семья. небольшая, но очень дружная: мама, папа, бабушка и я. Каждый из членов семьи заботится друг о друге, и, особенно, обо мне, и всегда придёт на помощь в трудную минуту, потому что в семье, по крайней мере, в моей, любовь друг к другу и поддержка, не смотря ни на что, всегда превыше всего. Правда, поддерживают пока меня, а не я их, но я люблю их всех очень сильно. Люблю приходить после уроков домой, и, открывая дверь, слышать их громкие голоса, а моя семья всегда очень громкая. Люблю, когда пахнет чем – то вкусненьким: значит мама готовит нам очередной шедевр. Ненавижу расстраивать свою семью, обожаю путешествовать с ними и собирать в памяти воспоминания. Когда началась пандемия и все мои друзья сходили с ума, я наслаждался каждой минутой, каждой игрой в лото по вечерам, каждым рассказом бабушки о своей молодости, особенно, когда ее глаза при этом наполнялись радостью и теплом. Вот оно – счастье! Это мои мама, папа и бабушка! Нет ничего в жизни важнее и роднее, чем моя семья! Я прочитал где-то о том, что семья – это ковчег спасения, и я с этим согласен. Ковчег спасения, где можно укрыться от всех проблем и найти поддержку и любовь. И я очень дорожу своим ковчегом!
Вопросы для обсуждения после прочтения текста։

1. А что для вас всего дороже на свете?
2. Как вы считаете, кто такие “дорогие” люди?
3. Есть ли для вас что-то дороже семьи?
4. Каким образом что-то становится важным и дорогим для нас?
   Прокомментируйте данные высказывания։

На свете должен быть кто-то, кому от тебя нужно лишь одно: чтобы ты был жив и чтобы у тебя все было хорошо.
Труды во имя близких не следует и почитать за труд.
Нет в этом мире радости сильней, чем лицезренье близких и друзей.
Не нужно, чтобы тебя любил весь мир. Достаточно нескольких близких людей.
Задания для выполнения։

1. Подберите синонимы к следующим словам:
   Важный, уютный, родной, хороший, радостный.
   
   Важный-значимый, серьезный, значительный, существенный.
   
   Уютный-комфортный, удобный, пригодный для проживания, уютивый.
   
   Родной-близкий, свой, домашний, родственный.
   
   Хороший-отличный, прекрасный, замечательный, качественный.
   
   Радостный-веселый, радужный, счастливый, умиротворенный.
   
2. Составтье словосочетания с данными словами:
   Добрая, удачное, сестра, жадный, внимательный, природа, дружелюбные, семья
   
   Добрая сестра.
   
   Удачное семейное счастье.
   
   Жадный внимательный взгляд.
   
   Природа дружелюбная.
   
   Семья внимательных и дружелюбных людей.
   
   3. Поставьте данные слова во множественное число։

друге
люди
цели
народы
сны
враги
игры
цветки

1.Բաց թողնված տառերը լրացրո՛ւ:

Մար.ուն իր ամբո.. կյան.ում ուղեկցում է ձայնը: Մար.ը բացար.ակ լռության պայմա..երում վատ է զգում. նրան պատում է  երկ..ղի ու անհարմարության զգացում: Բացար.ակ լռությունը խա.արում է մար.ու ն..րդային համակարգն այնպես, ինչպես և անվեր. աղմուկը: .րոտը, հրաբու.ների ձայնը, ծովային մ..իկները և այլ աղմուկներ անհանգստացնում են մարդուն: Կան բնական աղմուկներ .լ, ինչպես թռ.ու..երի դայլայլը, ա..յուրների կարկաչ..նը, ծովի ալիքների համ.նթաց ճողփ..նը, հաճելի են մար.կանց համար, բարերար են ներգործում նրանց ն..րդային համակար.ի վրա: Տհաճ աղմուկը քայքայում է մար.ու առո..ությունը: Աղմուկի հետ են կապվում լսողության կորուստը, ն..րդահոգեկան հիվանդությու..երի աճը, ֆիզիկական և մտա.որ ըն.ունակություն.երի նվազումը:

Մարդուն իր ամբողջ կյանում ուղեկցում է ձայնը: Մարդը բացարձակ լռության պայմաներում վատ է զգում, նրան պատում է երկղի ու անհարմարության զգացում: Բացարձակ լռությունը խաղարում է մարդու նարդային համակարգը, այնպես ինչպես անվերջ աղմուկը: Կան բնական աղմուկներ, որոնք լինեն թռչուկների դայլայլը, արյուրների կարկաչնը, ծովի ալիքների համանթաց ճողփնը, հաճելի են մարդկանց համար, բարերար են ներգործում դրանց նարդային համակարգի վրա: Թհաճ աղմուկը քայքայում է մարդու առողջությունը: Աղմուկի հետ են կապվում լսողության կորուստը, նարդահոգեկան հիվանդություների աճը, ֆիզիկական և մտավալը, ինչպես նարդահոգեկան երկրի նվազումը:

2․ Երկու տեքստ ստացի՛ր` կետերի փոխարեն գրելով տրված հոմանիշներից նախ առաջինը, ապա` երկրորդը: Ստացված տեքստերը համեմատի՛ր:

Ամպրոպի ժամանակ եղե՞լ է այնպիսի … (առիթ, դեպք), որ կայծակի … (կարճատև, վայրկենական) … (բռնկման, բոցի) լույսով… (դիտելու, տեսնելու) աշխույժ փողոցի … (տեսարանը, տեսքը): Այդ ժամանակ … (անշուշտ, անպայման)… (նկատած, տեսած) կլինեք կայծակի մի … (տարօրինակ, անսովոր) … (առանձնահատկությունը, կողմը), փողոցը … (անշարժացած, քարացած) է թվում, ձիերը կանգ են առել …(պրկված, լարված) դիրքերով` ոտքերը օդում պահած, կառքերը կանգնել են, պարզ երևում է անիվի … (յուրաքանչյուր, ամեն մի) ճաղը…։ Այդ… (թվացյալ, թվացող) անշարժության պատճառը կայծակի … (աննշան, փոքր) տևողությունն է: Կայծակը, ինչպես ամեն մի էլեկտրական կայծ, … (չափազանց, շատ) կարճ է տևում, նրա տևողությունը նույնիսկ չի կարելի չափել սովորական … (եղանակներով, ձևերով):

Ամպրոպի ժամանակ եղե՞լ է այնպիսի առիթ, որ կայծակի կարճատև բռնկման լույսով դիտելու աշխույժ փողոցի տեսքը: Այդ ժամանակ անշուշտ նկատած կլինեք կայծակի մի առանձնահատկությունը, փողոցը անշարժացած է թվում, ձիերը կառքերով պահած են, ոտքերը օդում պահած, կառքերը կանգնել են, պարզ երևում է անիվի յուրաքանչյուր ճաղը: Այդ թվացյալ անշարժության պատճառը կայծակի աննշան տևողությունն է: Կայծակը, ինչպես ամեն մի էլեկտրական կայծ, չափազանց կարճ է տևում, նրա տևողությունը նույնիսկ չի կարելի չափել սովորական եղանակներով:

Առաջադրանքներ կրկնողության համար

1. 

ա)x⁴y⁴
բ)1000a³
գ)27bc³
դ) x^3y^3z^3
ե) 16a^2b^2c^2
զ) 256a^4 b^4
է) 32+a^5+b^5
ը) 3a^2

2.

ա) 8 x^2 y^4
բ) a^4 b^3
գ) a^5 b^4 c^3
դ) 9 x^3 y^5 z^2
ե) a^4 x^4
զ) a^6 b^5
3.

ա) (ab)^4
բ) (3x)^3
գ) (0,245b)^2
դ) (-2xy)^3
ե) (3xy)^4
զ) (2y)^5
ի) (2a)^4
լ) (4a)^2
թ) (2m)^3
4.

ա) a^12
բ) x^10
գ) x^5 y ^3 z
դ) b^2 c^4 d^8
ե) 9 a^6
5.

ա) a^11:a^4=a^7
բ) a^5:a^3=a^2
գ) a^9:a^6=a^3
դ) a^n+1:a^2
ե) a^3.a^5=a^8
զ) a^2.a^7=a^9
6.

ա) y^8 x^12
բ) 8 a^6
գ) 2t a^6
7.

ա) 6a^2 b
բ) 8 b^2 c^5
գ) 9 c^2 t^3
դ) 14 x^4 y^5
ե) 6 x^4 y^4
զ)25!a⁵0

Խառը խնդիրներ ուղղանկյան, զուգահեռագծի, սեղանի վերաբերյալ

1. Ուղղանկյան կից կողմերը 12սմ և  25սմ են։ Գտեք ուղղանկյան պարագիծը։

P = 2*(25+12) = 2*(37) = 74 սմ:

2. AD և BC հիմքերով սեղանի մեջ AB=CD։ Ինչպիսի՞ սեղան է  ABCD-ն։

Եթե AD և BC հիմքերով սեղանի մեջ AB = CD, այս դեպքում ABCD սեղանը կոչվում է ուղղանկյան, քանի որ այն ունի երկու հավասար կողմեր ու երկու ծայրեր, որոնց հավասարությունը հավասար է։

3. O-ն   ABCD զուգահեռագծի անկյունագծերի հատման կետն է։ Ի՞նչ է   AO-ն  ABD եռանկյան համար։

Եթե O-ն է ABCD զուգահեռագծի անկյունագծերի հատման կետը, ապա AO-ն կլինի ABD եռանկյան բարձրության համար, որը հավասար է OՑՈՒ և AO եռանկյան բարձրությանը։

4. Հավասարասրուն սեղանի սրունքը հավասար է փոքր հիմքին և մեծ հիմքից փոքր է երկու անգամ։ Գտեք սեղանի պարագիծը, եթե փոքր հիմքը 7 է։

AB + BC + CD + AD = 7 + 14 + 7 + 14 = 42
5.Ուղղանկյան պարագիծը 20 սմ է: Որքա՞ն կարող է լինել այդ ուղղանկյան կողմի առավելագույն երկարությունը: Ուղղանկյան կողմերի երկարությունները արտահատվում են ամբողջ թվերով:

20 / 4 = 5 cm
6. Քանի՞ ուղիղ անկյուն ունի ուղղանկյուն սեղանը։
2

7. BC և   AD  հիմքերով ուղղանկյուն սեղանում  <B=90^0 է,  C կետից տարված է CK  բարձրությունը։ Ապացուցեք, որ AK=BC:

ABCD ուղղանկյանը սեղանատեր է, այդպիսով BCK եռանկյան բարձրությունը կլինի BK = CK։

8.Ուղղանկյան պարագիծը 60սմ է։ Գտեք ուղղանկյան կողմերը, եթե նրա կից կողմերը հարաբերում են ինչպես 1:9-ի։

մեծ կողմը = 9x = 9 * 6 = 54 սմ, փոքր կողմը = x = 6 սմ։

9. ABCD ուղղանկյան անկյունագծերը հատվում են О կետում։ Գտեք АОB եռանկյան պարագիծը, եթե <CAD=30^0, АC=12 սմ։

AB + BC + AC = 2x + x + 12 = 3x + 12

10. Գտեք ABCD ուղղանկյան պարագիծը, եթե  A  անկյան կիսորդը տրոհում է  BC կողմը   45, 6սմ և  7, 85սմ երկարությամբ հատվածների։

60^օ, 60^օ, 130^օ, 130^օ

11. ABCD զուգահեռագծի B  գագաթից АD կողմին տարված է  BH բարձրությունը, որ AB կողմի հետ կազմում է 40 աստիճանի անկյուն։ Գտեք զուգահեռագծի բոլոր անկյունները։

20սմ, 30սմ, 20սմ, 30սմ,

12. Զուգահեռագծի պարագիծը 100սմ է:Նրա կողմերից մեկը մյուսից մեծ է 10սմ-ով:Գտեք զուգահեռագծի կողմերը:

65^օ, 115^օ, 65^օ, 115^օ

13. Զուգահեռագծի անկյուններից մեկը 50 աստիճանով մեծ է մյուսից:Գտեք զուգահեռագծի անկյունները:
14. O-ն   ABCD զուգահեռագծի անկյունագծերի հատման կետն է: Գտեք BO -ն և OC-ն, եթե  BD=12, AC=17։

OC = 8.5
BO = 6։