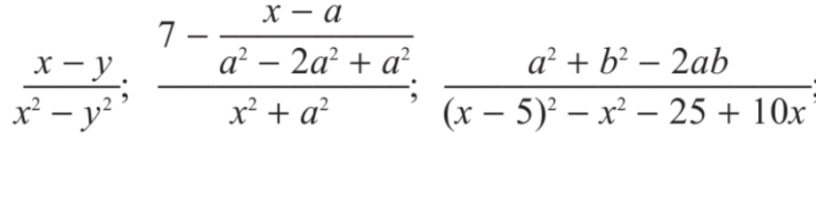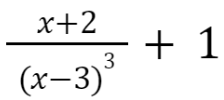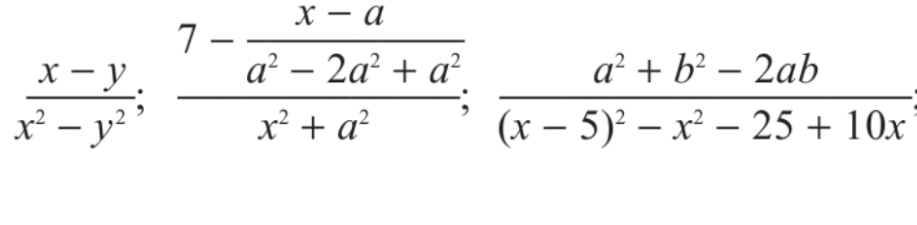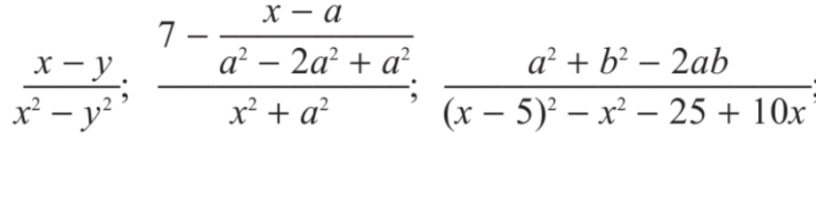
Թեմա՝ Ռացիոնալ արտահայտություն և նրա թվային արժեքը։ Վարժությունների լուծում։
ա) a + b / ab
բ) 1 / (a + b)^2
գ) (ab)^2 / a^2 + b^2
դ) a / a^2 + 1
2. Հաշվել.
ա) 3 / 10
բ) 1 / 36
գ) 1 / 8
3. Տառերի ինչպիսի՞ արժեքների դեպքում է որոշված արտահայտությունը
ա) a-ն հավասար չէ 0-յի
բ) x-ն հավասար չէ 1-ի
գ) c-ն հավասար չէ -3-ի
դ) a-ն հավասար չէ 3-ի
4. Գտնել արտահայտության արժեքը.
ա) 0.96
բ) 2.5
գ) -4
դ) -91/-9
5. Գտնել արտահայտության արժեքը.
ա) 1 / 10
բ) 2
Թեմա՝ Ռացիոնալ արտահայտություններ և դրանց թվային արժեքը:
Ռացիոնալ արտահայտություն կոչվում է այն արտահայտությունը, որում մի քանի հանրահաշվական կոտորակներ միացված են թվաբանական գործողությունների նշաններով:
Ընդ որում այդ արտահայտությունը չպետք է պարունակի զրոյական բազմանդամի վրա բաժանման գործողություն:
Հանրահաշվական կոտորակը նույնպես անվանում են ռացիոնալ արտահայտություն:
Օրինակ․
Ռացիոնալ են հետևյալ արտահայտությունները՝
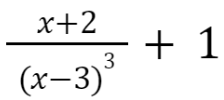
Որպեսզի այսպիսի արտահայտությունները ճիշտ պարզեցնել, պետք է՝
Օրինակ՝
Հարցեր և առաջադրանքներ:
Ռացիոնալ արտահայտություն կոչվում է այն արտահայտությունը, որում մի քանի հանրահաշվական կոտորակներ միացված են թվաբանական գործողությունների նշաններով:
2. Պարզեցնել ռացիոնալ արտահայտությունը.
ա) bc+ac+ab
բ) 15x2-5x+5
3. Արտահայտություններից որո՞նք իմաստ չունեն.
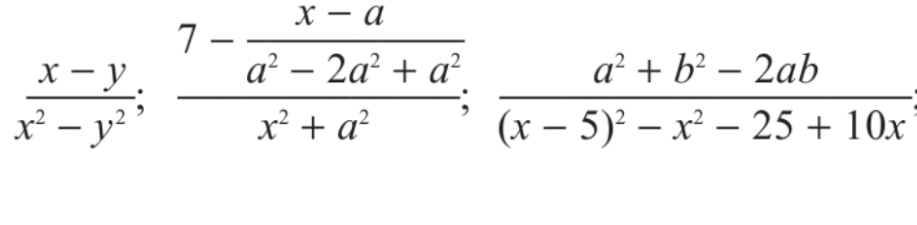
երկրորդը և երրորդը իմաստ չունեն
4.x-ի ինչպիսի թվային արժեքի համար հանրահաշվական կոտորակի արժեքը հավասար է 0-ի.
ա) x = 2
բ) x = -4
գ) x = 2
դ) -2.5
ե) 0
5. Գտնել արտահայտության արժեքը, երբ x=2
ա) x = 2
բ) x = -4
գ) x = 2
դ) -2.5
ե) 0
6. Հաշվել արտահայտության արժեքը.
ա)10/3
բ)-237/25
գ)-5/3
Թեմա՝՝ Վարժությունների լուծում
ա) x+3y-1=-x+4y+8
2x-y-9=0
-y=9-2x
y=-9+2x
x+3(2x-9)-1=0
x+6x-27-1=0
7x=28
x=4
y=-9+8=-1
y=-1
(4;-1)
բ)x-2y+3=-x+3y-2
2x -5y+5=0
-5y=-2x-5
y=(2x+5)/5
x-4x+10/5+15=0
x+25=0
x=-25
y=-9
(-25;-9)
գ)x-y+2=3x+y-4
2x+2y-6=0
x+y-3=0
x=3-y
3-y-y-2=0
-2y=-1
y=0.5
x=2.5
(2.5;0.5)
դ) 2x+y-3=-x-y+4
3x+2y-7=0
y=7-3x/2
2x+7-3x-3/2=0
4x+7-3x-6/2=0
x+1=0
x=-1
y=5
(-1;5)
2. Լուծել հավասարումների համակարգը տեղադրման եղանակով.
ա) x=3-2y
3-2y+y+1=0
-y=-4
y=4
x=3-8=-5
x=-5
(-5;4)
բ) x=3y-3
3y-3+y=1
4y=4
y=1
x=3-3=0
(0; 1)
գ) y=2-4x
3x+2-4x+3=0
-x=-5
x=5
y=2-20=-18
y=-18
(5;-18)
դ) x=y+7
21+3y-y+1=0
2y=-22
y=-11
x=-11+7=-4
x=-4
(-4;-11)
3. Ձևափոխել հանրահաշվական կոտորակի.
ա) 2a+3b/6
բ) x-2y/4
գ) 10m-12/15
դ) 20m+6n/15=2(10m+3n)/15
ե) 17p/12
զ) 3a2-8a/12=a(3a-8)/12
է) 74x2/15
ը) 54xy-35xy2/63=xy(54-35y)/63
4. Ձևափոխել հանրահաշվական կոտորակի.
ա) 2x-3/x3
բ) 7-3am2/m4
գ) ab7+a5b3/(a5b5)(ab7)
դ) 4x2b5-3x4b3/x6b8
ե) 3a(xy4z)-3b(x7y5z)/x8y9z6
զ) m7n*a3*b6*c4+3m2*a4b3c4/a7b9c13
5. Կատարել գործողությունները.
ա) a+1/7x*2x/a+1=2/7
բ) 2/3n
գ) 2/p
դ) 2ab
ե) 4
զ) 12(a-b)/5a2b2
Ռոբերտ Մխիթարյան 