Թեմա՝ Երեք անհայտով հավասարումների համակարգեր:
ax + by + cz + d=0 տեսքի հավասարումը, որտեղ a, b, c և d-ն տրված թվեր են, ընդ որում a, b, c թվերից , գոնե մեկը 0-ից տարբեր է, անվանում են երեք անհայտով առաջին աստիճանի հավասարում։ (x0,y0, z0) թվերի եռյակը անվանում են հավասարման լուծում, եթե այդ թվերը բավարարում են հավասարմանը, այսինքն եթե հավասարման մեջ x-ի փոխարեն տեղադրում են x0 , y-ի փոխարեն տեղադրում են y0 , z-ի փոխարեն՝ z0 հավասարումը դառնում է ճիշտ թվային հավասարություն` ax0+by0+cz0+d=0
Դիտարկենք երեք անհայտովհավասարումների համակարգի լուծման օրինակներ և ցույց տանք, որ այդ համակարգերը կարելի է լուծել տեղադրման եղանակով։ Օրինակ․ Լուծենք հետևյալ հավասարումների համակարգը՝
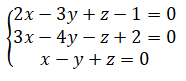
Համակարգի երրորդ հավասարումից x-ն արտահայտենք y և z-ով` x= y-z և y-z-ը x-ի փոխարեն տեղադրենք համակարգի առաջին և երկրորդ հավասարումների մեջ։ Կստանանք՝

հավասարումները, որոնք նման ամդամների միացումից հետո կգրվեն այսպես`

Այսպիսով,տեղադրման եղանակով կարելի է x, y և z երեք անհայտով երեք առաջին աստիճանի հավասարումների համակարգի լուծումը բերել y և z երկու անհայտով երկու առաջին աստիճանի երկու հավասարումների համակարգի լուծման։ Լուծելով վերջին համակարգը՝ գտնում ենք, որ y0=-2, z0=1։ y0-ի և z0-ի արժեքները տեղադրելով x=y-z արտահայտության մեջ՝ գտնում ենք, որ x0=-3 ։ Այսպիսով, համակարգն ունի միակ լուծում` x0=-3, y0=-2, z0=1։ Պատ․՝ (-3;-2;1)
Օրինակ 1

Օրինակ 2
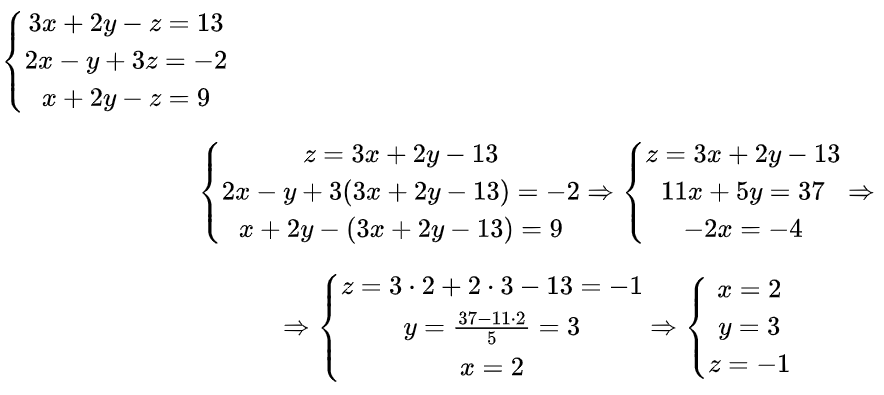
Օրինակ 3
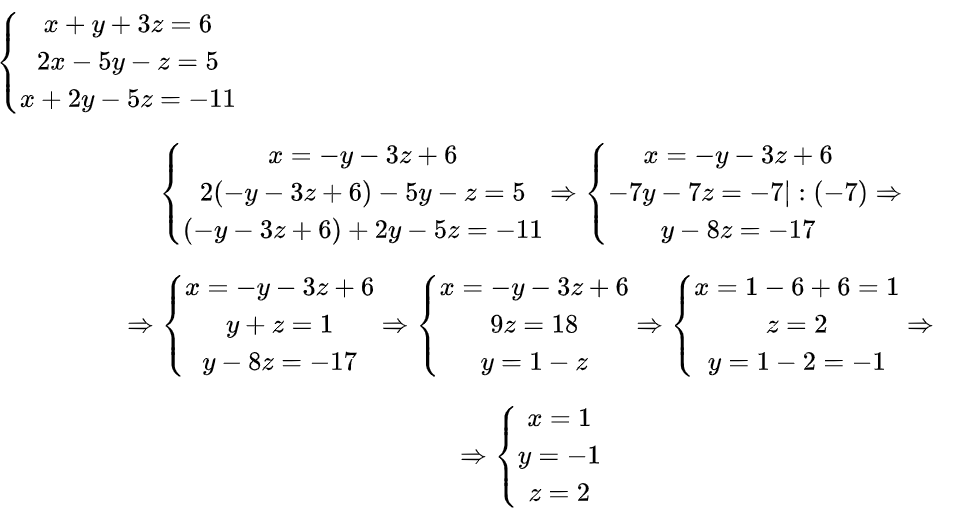
Գծային հավասարումների համակարգերի լուծման համար կիրառում են նաև Գաուսի մեթոդը։ Օրինակով դիտարկենք այդ մեթոդը։ Լուծենք հետևյալ հավասարումների համակարգը՝

Երրորդ հավասարումից գտնում ենք ՝ z=3։ Երկրորդ հավասարման մեր z-ի փոխարեն տեղադրելով 3՝ գտնում ենք՝ y=2։ Վերջապես առաջին հավասարման մեջ z-ի փոխարեն տեղադրելով 3, իսկ y-ի փոխարեն 2, գտնում ենք՝ x=1։ Այսպիսով , համակարգն ունի միակ լուծում ` (1;2;3) Այս տեսքի հավասարումների համակարգերն անվանում են «եռանկյունաձև» տեսքի հավասարումների համակարգեր։
Առաջադրանքներ։
1․ Լուծել հավասարումների համակարգը․

ա) {x=1
{3x+2y-3z=2
{5x-y-5z=-1
3+2y-3z=2
5-y-5z=-1
3+2y-3z=2
5-y-5z=-1
2y-3z=-1
-y-5z=-6
-y=-6+5z
y=(6-5z)
2(6-5z)-3z=1
12-10-32=-1
-13z=-1-12
-13z=-13
z=1
{x, y, z=1
բ)
y=12:3=4
x+4+z=7
x-8+2z=-3
y=4
x=3-z
3-z-8+2z=-3
z=-3-3+8=2
{y=4
{x=3-z
{z=2
{y=4
{x=3-2=1
{z=2
գ)
{6y-2y-z=1
{10y+4y-2z=8
{4y-z=1
{14y-2z=8
{z=-1+4y
{14y-2*(-1+4y)=8
14y+2-8y=8
6y=6
y=1
x=2×1=2
z=-1+4*1
z=3
{x=2
{y=1
{z=3
{x=(5-y)
{3*(5-y)-2y+z=6
{5-y-5y+3z=-4
{x=5-y
{-5y+z=-11
{-6y+3z=-9
z=-11+5y
-6y-3z+15y=-9
-6y-3*(-11+5y)+15y=9
-6y=-9-33
y=7
z=-11+5*7
z=24
x=5-y=5-7=-2
{x=-2
{y=7
{z=24
2․ Լուծել «եռանկյունաձև» տեսքի հավասարումների համակարգը․

ա) {x-4*3=2
{x=14
բ) x=-7
2*(-7)-3y=1
-14-3y=1
-3y=-15
y=5
x=-7
y=5
գ) x=3
-3*3+5y=16
-9+5y=16
5y=16+9=25
y=25:5=5
x=3
y=5
դ) 4y-3*2=2
3x+4y-6*2=2
4y-6=2
4y=2+6=8
y=8:4=2
3x+4*2-6*2=2
3x+8-12=2
3x=6
x=2
x=2
y=2
z=2
ե) x=-3
3*(-3)-y=0
y=9
3+9-z=-6
-z=-6-12
z=18
x=-3
y=9
z=18
զ) x=5
4*5-3y=5
-3y=20-5=15
y=-5
-5-5+z=5
z=15
x=5
y=-5
z=15
3․ Լուծել հավասարումների համակարգը․
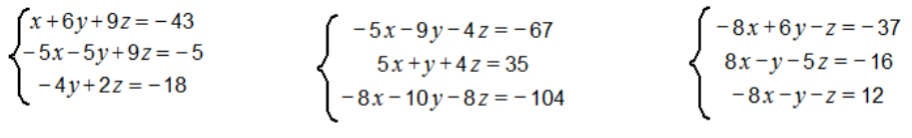
2z=-18+4y
z=2y-9
x+6y+9(2y-9)=-43
x+6y+18y-81=-43
x+24y=38
x=38-24y
-5(38-24y)-5y+9(2y-9)=-5
-190+120y-5y+18y-81=-5
133y=266
y=2
x=-10
z=-5
-4x-5y-4z=-52
4z=67-5x-9y
4z=35-5x-y
4z=52-4x-5y
67-5x-9y = 35-5x-y
67-9y=35-y
8y=32
y=4
35-5x-y=52-4x-5y
35+4y=x+52
35+16=x+52
x+52=51
x=-1
4z=35+5-4
4z=36
z=9
8x=37+6y-2
8x=y+5z-16
8x=-12-y-2
37+6y-z=-12-y-z
37+6y=-12-y
7y=-37-12
7y=-49
y=-7
